Spinning particles:
Semiclassical quantisation and spectral statistics

Summary

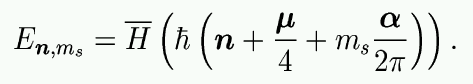
Chapter 2 provides an overview of semiclassical methods for systems with spin, as developed in [BK98,Kep98,BK99a]. It turns out that in a semiclassical treatment of systems which are described by the Pauli or the Dirac equation translational and spin dynamics contribute in different ways. Firstly one requires solutions of the classical point particle dynamics, which are not influenced by the spin degree of freedom. On the other hand one also has to integrate a classical equation of spin precession along these solutions. For the subsequent treatment it is useful to combine these two dynamics in terms of a skew product, which is defined on the product of the phase space of the translational degrees of freedom and the sphere. The latter represents the phase space associated with the spin degree of freedom.

In chapter 3 we analyse the properties of this skew product in detail. In particular, we extend the notion of integrability from the case of Hamiltonian systems to the situation at hand. In Theorem 3.4.4 we specify a sufficient condition for integrability and derive its consequences. In this context the following geometrical construction plays an important role: The time evolution of an integrable skew product of translational and spin degrees of freedom takes place on fibre bundles over Liouville-Arnold tori, and the fibres can be embedded into the sphere as parallels of latitude, cf. fig. 3.3.

In chapter 4 we derive explicit semiclassical quantisation conditions for integrable systems with spin. The construction of the semiclassical eigenfunctions relies heavily on the results presented in chapter 3. If we denote by H(I) the Hamiltonian of the translational degrees of freedom, expressed in action and angle variables (I,θ), then the semiclassical energy eigenvalues are given by

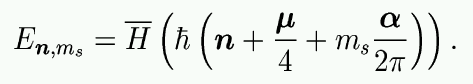
Here h denotes Planck's constant h divided by 2π, the components of n=(n₁,...,n_d) are integers, and the Maslov indices μ are known from Einstein-Brillouin-Keller (EBK) quantisation [Kel58]. The last term in the bracket represents the influence of the spin. Here m_s=-s,...,s (s ∈ 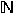/2) denotes a spin quantum number and the rotation angles α can be calculated from classical spin precession along the closed paths on Liouville-Arnold tori.

Chapter 5 is dedicated to the derivation of classical sum rules for the skew product of translational and spin degrees of freedom. Classical sum rules express certain weighted averages along periodic orbits as phase space averages. They are an important tool for the semiclassical analysis of spectral statistics. Technically, one obtains classical sum rules by investigating the trace of a classical time evolution operator. For systems with spin we show that the choice of the Hilbert space on which this operator is defined plays an important role: it distinguishes between particles with different spin (e.g., spin s=½ or s=1), whereas the classical dynamics remains the same.

In chapter 6 we investigate spectral correlations, building on the methods and results of chapters 2 and 5. Depending on the properties of the corresponding classical systems (e.g. chaotic or integrable dynamics) one expects different spectral statistics (derived from random matrix theory or described by a Poisson process, respectively). For chaotic systems one also has to distinguish between different symmetry classes. In the case of chaotic systems we generalise known results [HO84,Ber85] to the case of the symplectic universality class which is only found for systems with half-integer spin (section 6.3.2). For regular dynamics we show that the novel notion of integrability defined in chapter 3 is a necessary prerequisite in order to obtain universal correlations according to a Poisson process (section 6.3.3). Between these two extremes we identify the interesting case of systems whose translational dynamics are integrable but the skew product of translational and spin degrees of freedom does not satisfy the conditions of Theorem 3.4.4. In this situation we semiclassically find intermediate statistics (section 6.3.4), which may be related to new "universality" classes which were defined only recently [BGS01].

Various results from this work are illustrated in an introductory chapter (chapter 1) in terms of simple toy models.

Literature:

[Ber85]	M. V. Berry,
	Semiclassical theory of spectral rigidity,
	Proc. R. Soc. London Ser. A 400 (1985) 229-251.
[BGS01]	E. B. Bogomolny, U. Gerland and C. Schmit,
	Short-range plasma model for intermediate spectral statistics,
	Eur. Phys. J. B 19 (2001) 121-132.
[BK98]	J. Bolte and S. Keppeler,
	Semiclassical Time Evolution and Trace Formula for Relativistic Spin-½ Particles,
	Phys. Rev. Lett. 81 (1998) 1987-1991.
[BK99a]	J. Bolte and S. Keppeler,
	A Semiclassical Approach to the Dirac Equation,
	Ann. Phys. (NY) 274 (1999) 125-162.
[HO84]	J. H. Hannay and A. M. Ozorio de Almeida,
	Periodic orbits and the correlation function for the semiclassical density of states,
	J. Phys. A 17 (1984) 3429-3440.
[Kel58]	J. B. Keller,
	Corrected Bohr-Sommerfeld Quantum Conditions for Nonseparable Systems,
	Ann. Phys. (NY) 4 (1958) 180-185.
[Kep98]	S. Keppeler,
	Semiklassik für Dirac-Teilchen,
	Diplomarbeit, Universität Ulm, 1998.